» no hay suficiente amor y bondad en el mundo para permitir regalar nada de eso a seres imaginarios.»- Friedrich Nietzsche
a veces, si quieres describir el universo en el que vives con precisión, necesitas ir más allá de las formas convencionales de pensar. A principios del siglo 20, dos revoluciones en la física — la relatividad de Einstein (primero especial, luego general) y la mecánica cuántica — trajeron la necesidad de las matemáticas más allá de lo que los números reales podrían traernos solos., Desde entonces, las matemáticas complejas, que consisten en partes reales e imaginarias, se han entrelazado inextricablemente con nuestra comprensión del Universo.

matemáticamente, cuando pensamos en números, podemos pensar en algunas formas diferentes de categorizarlos:
- Los números contables: 1, 2, 3, 4, etc., Hay un número infinito de estos.
- Los números enteros: 0, 1, 2, 3, etc. Estos son los mismos que los contables, pero también incluyen cero.
- Los enteros: …, -3, -2, -1, 0, 1, 2, 3, etc. Puede que no parezca mucho, pero el reconocimiento de que podemos tener números negativos fue enorme, y que puede haber tantos negativos como positivos. Esto incluye todos los números enteros, así como sus negativos.
- Los racionales: cualquier número que se puede expresar como una fracción de un entero sobre otro., Esto incluye todos los enteros (que pueden expresarse como ellos mismos sobre uno), así como un número infinito de racionales entre cada entero. Cualquier decimal que se repita infinitamente puede expresarse como un número racional.
- Los Reales: incluye todos los racionales, así como todos los números irracionales, como las raíces cuadradas de cuadrados no perfectos, π, y toda una serie de otros. La suma de cualquier número racional y cualquier número irracional será irracional, pero las sumas de dos irracionales pueden ser racionales.,
pero, mientras que la raíz cuadrada de un número positivo es real, la raíz cuadrada de un número negativo no está bien definida.

al menos, no lo era, hasta que los definimos, e inventamos los números imaginarios para hacer exactamente eso! Un número imaginario es igual que uno real, excepto que se multiplica por «i», o la raíz cuadrada de (-1)., Los números también pueden ser complejos, donde tienen una parte real (a) y una parte imaginaria (b), y normalmente se expresan como (a + bi).
ahora que sabes lo que son, Aquí están mis 5 Datos divertidos sobre números imaginarios!
1.) La raíz cuadrada de I tiene partes reales e imaginarias. ¡La raíz cuadrada de un número real negativo es puramente imaginaria, pero la raíz cuadrada de un número puramente imaginario tiene que tener partes reales e imaginarias! Así es como puedes demostrártelo a ti mismo. Necesita algún número, cuadrado, igual √(-1)., Imagine que podría tener una parte real, x, y una parte imaginaria, y, por lo que podríamos escribir como (x + yi). Entonces podríamos averiguar lo que X E y necesitan ser para que esto funcione.,

así que nos cuadrado ambos lados,

y ahora vamos a coincidir la parte real con la parte real, y la parte imaginaria con la parte imaginaria., podemos resolver para y:

Como puede ver, hay dos posibles soluciones, y si hacemos uso de la mano derecha (parte imaginaria) de la ecuación a resolver para x (que resulta ser igual y en ambos casos), obtenemos dos soluciones:

lo Que nos lleva a la siguiente hecho de la diversión…
2.,) Cualquier raíz de I tiene múltiples soluciones únicas, y la raíz n-ésima tiene N soluciones únicas. Para números positivos, reales, tomar la raíz cuadrada (es decir, la segunda raíz) de ese número le da dos soluciones posibles: una positiva y una negativa. Por ejemplo, √(1) puede ser +1, o puede ser -1, ya que uno al cuadrado le dará 1.
Pero para i, o √(-1), si quieres tomar raíces de eso, tienes que hacer una ecuación polinómica, como hicimos anteriormente. La cosa es, el orden de la ecuación polinómica depende de qué raíz tomamos de ella., Así que el tercer, cuarto y quinto raíces de tengo que satisfacer:

Y habrá tres, cuatro, y cinco soluciones únicas (respectivamente) para cada una de las x y de y en estas ecuaciones., Por ejemplo, las tres soluciones para los cubos (3º) de la raíz de i son:

(Prueba de medición de volumen de todos estos, y ver por ti mismo!) Y eso ni siquiera se trata de fracciones, que son toda otra lata de gusanos. De hecho…
3.) En una fracción imaginaria, realmente importa si el numerador o denominador tiene la » i » en ella., Si piensas en el número (-1), no importa si lo piensas, en términos fraccionales, como(-1)/1 o como 1/(-1); sigue siendo el número (-1) de cualquier manera. Pero ese no es el caso para mi! Déjame preguntarte esto: ¿qué crees que es esta fracción?

Buscando, usted podría pensar que es igual a i, pero, en realidad, de -i!
¿quieres probarlo?, Simplemente multiplique la parte superior e inferior por i, y ver por ti mismo:

La cosa tiene que ser muy cuidadoso acerca de es que al combinar o separar las raíces cuadradas de los números negativos, hay intrincadas reglas que debe seguir para obtener correcto. Las violan, y usted puede hacer todo tipo de locuras, como demostrar que +1 y -1 son iguales el uno al otro.,

En cambio, la matemática subyacente detrás de cómo combinarlos nos muestra una cosa realmente extraña
4.) e, π, e i están todos relacionados entre sí., Usted sabe que si usted tiene su estándar de x-y-ejes (real), también puede representar que coordinan el espacio mediante coordenadas polares, donde se tiene una coordenada radial (r) y un ángulo polar (θ), así:
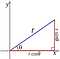
bueno, si creas, en lugar de un eje x E y, un eje real e imaginario, puedes hacer lo mismo, excepto que esta vez el ángulo θ te lleva desde el plano real al plano imaginario y de vuelta otra vez!

lo más sorprendente de esto es que si que vaya a la posición de -1 en el eje real, llegamos a una bonita identidad:

No es: una simple e inesperada relación entre e, i, y π. Estas relaciones aparecen mucho en análisis complejos. Y sin embargo, si estás dispuesto a considerar exponenciales, este último es un doozy
5.) I^i, O he elevado al poder i, es 100% real., Piense en la ecuación en la imagen de arriba-la fórmula de Euler – pero en lugar de dirigirse a (-1) en el eje real, vamos a ir a i en el eje imaginario en su lugar.,d=»952eecae59″>
Así, si queremos saber lo que i^i es, todo lo que tenemos que hacer es elevar ambos lados de esta ecuación con el poder,

y recuerda que i^2 = -1, y nos encontramos con que:

que se acerca a ~0.,20788, un número puramente real. ¡Y esos son mis 5 hechos matemáticos divertidos sobre números imaginarios!




