“Non c’è abbastanza amore e bontà nel mondo per permettere di dare nulla di tutto ciò agli esseri immaginari.”- Friedrich Nietzsche
A volte, se vuoi descrivere l’Universo in cui vivi con precisione, devi andare oltre i modi di pensare convenzionali. Nella prima parte del 20 ° secolo, due rivoluzioni in fisica — la relatività di Einstein (prima speciale, poi generale) e la meccanica quantistica — portarono la necessità della matematica oltre ciò che i numeri reali potevano portarci da soli., Da allora, la matematica complessa, composta da parti reali e immaginarie, è stata inestricabilmente intrecciata con la nostra comprensione dell’Universo.

Matematicamente, quando pensiamo ai numeri, possiamo pensare ad alcuni modi diversi per classificarli:
- I numeri numerabili: 1, 2, 3, 4, ecc., Ce ne sono un numero infinito.
- I numeri interi: 0, 1, 2, 3, ecc. Questi sono gli stessi dei numerabili, ma includono anche zero.
- Gli interi: …, -3, -2, -1, 0, 1, 2, 3, ecc. Potrebbe non sembrare molto, ma il riconoscimento che possiamo avere numeri negativi è stato enorme, e che ci possono essere tanti negativi quanti ce ne sono di positivi. Questo include tutti i numeri interi così come i loro negativi.
- I razionali: qualsiasi numero che può essere espresso come una frazione di un intero rispetto ad un altro., Questo include tutti gli interi (che possono essere espressi come se stessi su uno) e un numero infinito di razionali tra ogni intero. Qualsiasi decimale infinitamente ripetuto può essere espresso come un numero razionale.
- I reali: include tutti i razionali e tutti i numeri irrazionali, come le radici quadrate dei quadrati non perfetti, π e tutta una serie di altri. La somma di qualsiasi numero razionale e qualsiasi numero irrazionale sarà irrazionale, ma le somme di due irrazionali possono essere razionali.,
Ma, mentre la radice quadrata di un numero positivo è reale, la radice quadrata di un numero negativo non è ben definita.

Almeno, non lo era, finché non li abbiamo definiti e abbiamo inventato i numeri immaginari per fare esattamente questo! Un numero immaginario è proprio come uno reale, tranne che è moltiplicato per “i”, o la radice quadrata di (-1)., I numeri possono anche essere complessi, dove hanno sia una parte reale (a) che una parte immaginaria (b), e sono normalmente espressi come (a + bi).
Ora che sai cosa sono, ecco i miei primi 5 fatti divertenti sui numeri immaginari!
1.) La radice quadrata di i ha sia parti reali che immaginarie. La radice quadrata di un numero reale negativo è puramente immaginaria, ma la radice quadrata di un numero puramente immaginario deve avere sia parti reali che immaginarie! Ecco come puoi dimostrarlo a te stesso. Hai bisogno di un numero, al quadrato, uguale √(-1)., Immagina che potrebbe avere una parte reale, x, e una parte immaginaria, y, in modo che potremmo scriverla come (x + yi). Quindi potremmo capire cosa devono essere x e y perché funzioni.,

così abbiamo quadrato entrambi i lati,

e ora abbiamo abbinare la parte reale con la parte reale, e la parte immaginaria con la parte immaginaria., siamo in grado di risolvere per y:

Come si può vedere, ci sono due possibili soluzioni, e se usiamo la mano destra (parte immaginaria) della equazione da risolvere per x (che risulta pari a y in entrambi i casi), si ottengono le due soluzioni:

il Che ci porta al prossimo fatto di divertimento…
2.,) Qualsiasi radice di i ha più soluzioni uniche e la radice N-esima ha N soluzioni uniche. Per numeri reali positivi, prendere la radice quadrata (cioè la seconda radice) di quel numero ti dà due possibili soluzioni: una positiva e una negativa. Ad esempio, √(1) può essere +1, o può essere -1, poiché uno al quadrato ti darà 1.
Ma per i, o √(-1), se vuoi radicarlo, devi creare un’equazione polinomiale, come abbiamo fatto sopra. Il fatto è che l’ordine dell’equazione polinomiale dipende da quale radice prendiamo di esso., Così il terzo, quarto, quinto e radici di i have a soddisfare:

E ci saranno tre, quattro, e cinque soluzioni uniche (rispettivamente) per ogni x e y in queste equazioni., Per esempio, le tre soluzioni per il cubo (3) radice dell’io sono:

(da Provare la cubatura, tutti questi, e vedere di persona!) E non si tratta nemmeno di frazioni, che sono un’altra lattina di vermi. Infatti
3.) In una frazione immaginaria, in realtà importa se il numeratore o il denominatore ha la “i” in esso., Se pensi al numero (-1), non importa se lo pensi, in termini frazionari, come(-1)/1 o come 1/(-1); è ancora il numero (-1) in entrambi i casi. Ma questo non è il caso per me! Lascia che ti chieda questo: cosa pensi che sia questa frazione?

Guardando, si potrebbe pensare che sia proprio uguale a i, ma in realtà -ho!
Vuoi dimostrarlo?, Basta moltiplicare alto e in basso da i, e guardate voi stessi:

La cosa che dovete essere molto attenti è che quando si uniscono o separano le radici quadrate di numeri negativi, ci sono intricate regole che si devono seguire per ottenere corretto. Violali e puoi fare ogni sorta di cose folli, come dimostrare che +1 e -1 sono uguali l’uno all’altro.,

Invece, la matematica alla base di come combinarli ci mostra una cosa davvero bizzarra
4.) e, π, e i sono tutti legati l’uno all’altro., Sapete che se avete il vostro standard di x-e-y (reale), si può anche rappresentare che spazio di coordinate polari in coordinate, in cui si dispone di un radiale di coordinate (r) e un angolo polare (θ), in questo modo:
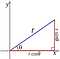
Bene, se crei, invece di un asse x e y, un asse reale e immaginario, puoi fare la stessa cosa, tranne che questa volta l’angolo θ ti porta dal piano reale al piano immaginario e viceversa!

La cosa sorprendente di questo è che se si naviga in posizione di -1 sull’asse reale, si arriva a una bella identità:

non C’è: un semplice e inaspettata relazione tra e, i, e π. Queste relazioni mostrano molto in analisi complesse. Eppure, se sei disposto a considerare gli esponenziali, quest’ultimo è un doozy
5.) i^i, o ho sollevato al potere i, è reale al 100%., Pensa all’equazione nell’immagine sopra — la formula di Eulero — ma invece di andare a (-1) sull’asse reale, andiamo invece a i sull’asse immaginario.,d=”952eecae59″>
Beh, se vogliamo sapere che cosa i^i è, tutto quello che dobbiamo fare è sollevare entrambi i lati di questa equazione per l’io, il potere,

e ricordate che i^2 = -1, e troviamo che:

che è su ~0.,20788, un numero puramente reale. E questi sono i miei primi 5 divertenti fatti matematici sui numeri immaginari!




