„nu există suficientă dragoste și bunătate în lume pentru a permite dăruirea oricărei ființe imaginare.”- Friedrich Nietzsche
uneori, dacă doriți să descrieți universul în care trăiți cu exactitate, trebuie să depășiți modurile convenționale de gândire. În prima parte a secolului 20, două revoluții în fizică — relativitatea lui Einstein (mai întâi specială, apoi generală) și mecanica cuantică — au adus nevoia de matematică dincolo de ceea ce numerele reale ne-ar putea aduce singuri., De atunci, matematica complexă, formată atât din părți reale, cât și imaginare, a fost strâns legată de înțelegerea noastră a Universului.

din punct de vedere Matematic, atunci când ne gândim la numere, ne putem gândi la câteva modalități diferite de a le clasifica:
- numărabile numere: 1, 2, 3, 4, etc., Există un număr infinit de acestea.
- numerele întregi: 0, 1, 2, 3 etc. Acestea sunt aceleași ca și contabilele, dar includ și zero.
- numerele întregi: …, -3, -2, -1, 0, 1, 2, 3, etc. Poate că nu pare prea mult, dar recunoașterea faptului că putem avea numere negative a fost una uriașă și că pot exista la fel de multe negative ca și cele pozitive. Aceasta include toate numerele întregi, precum și negativele lor.
- raționalele: orice număr care poate fi exprimat ca o fracție a unui număr întreg față de altul., Aceasta include toate numerele întregi (care pot fi exprimate ca ei înșiși peste unul), precum și un număr infinit de raționals între fiecare număr întreg. Orice zecimal care se repetă infinit poate fi exprimat ca un număr rațional.
- reals: include toate raționalele, precum și toate numerele iraționale, cum ar fi rădăcinile pătrate ale pătratelor non-perfecte, π și o mulțime de altele. Suma oricărui număr rațional și a oricărui număr irațional va fi irațională, dar sumele a doi iraționali pot fi raționale.,
dar, în timp ce rădăcina pătrată a unui număr pozitiv este reală, rădăcina pătrată a unui număr negativ nu este bine definită.

Cel puțin, nu a fost, până am definit-le, și a inventat numerele imaginare pentru a face exact asta! Un număr imaginar este la fel ca unul real, cu excepția faptului că este înmulțit cu „i”, sau rădăcina pătrată a (-1)., Numerele pot fi, de asemenea, complexe, unde au atât o parte reală (a), cât și o parte imaginară (b) și sunt în mod normal exprimate ca (a + bi).
acum, că știi ce sunt, aici sunt meu top 5 fapte amuzante despre numere imaginare!
1. Rădăcina pătrată a lui i are atât părți reale, cât și imaginare. Rădăcina pătrată a unui număr real negativ este pur imaginară, dar rădăcina pătrată a unui număr pur imaginar trebuie să aibă atât părți reale, cât și imaginare! Iată cum vă puteți dovedi. Aveți nevoie de un număr, pătrat, egal √(-1)., Imaginați-vă că ar putea avea o parte reală, x, și o parte imaginară, y, astfel încât să o putem scrie ca (x + yi). Apoi ne-am putea da seama ce x și y trebuie să fie pentru ca acest lucru să funcționeze.,

deci suntem chit ambele părți,

și acum avem meci la real, parte cu parte reală, și partea imaginară cu partea imaginară., putem rezolva pentru voi:

după Cum puteți vedea, există două soluții posibile, iar dacă vom folosi mana dreapta (partea imaginară) din ecuația de a rezolva pentru x (care se dovedește a egal y în ambele cazuri), avem două soluții:

ceea Ce ne aduce la următorul fapt amuzant…
2.,) Orice rădăcină a lui i are mai multe soluții unice, iar rădăcina A N-A are n soluții unice. Pentru numerele pozitive, reale, luând rădăcina pătrată (adică a doua rădăcină) a acelui număr vă oferă două soluții posibile: una pozitivă și una negativă. De exemplu, √(1) poate fi +1 sau poate fi -1, deoarece unul pătrat vă va da 1.dar pentru i, sau √(-1), dacă doriți să luați rădăcini, trebuie să faceți o ecuație polinomială, așa cum am făcut mai sus. Lucrul este că ordinea ecuației polinomiale depinde de ce rădăcină luăm din ea., Deci, al treilea, al patrulea, și al cincilea rădăcinile trebuie să satisfacă:

Și nu va fi de trei, patru, și cinci soluții unice (respectiv) pentru fiecare dintre x și y în aceste ecuații., De exemplu, cele trei soluții pentru cubed (3) rădăcină de mine sunt:

(Încercați cubaj toate acestea, și a vedea pentru tine!) Și nici măcar nu se ocupă de fracții, care sunt o altă cutie de viermi. De fapt…
3.) Într-o fracție imaginară, contează de fapt dacă numărătorul sau numitorul are „i” în el., Dacă vă gândiți la numărul (-1), nu contează dacă vă gândiți la el, în termeni fracționari, ca (-1)/1 sau ca 1/(-1); este totuși numărul (-1) oricum. Dar nu este cazul pentru mine! Permiteți-mi să vă întreb: ce credeți că este această fracțiune?

se Uită la ea, ai putea crede că e doar egal cu i, dar de fapt e -am!
vrei să-l dovedească?, Multiplica doar pe partea de sus și de jos mă, și vezi pentru tine:

Lucru trebuie să fie foarte atent despre este că atunci când se combină sau se separă rădăcinile pătrate ale numerelor negative, există reguli complicate trebuie să urmați pentru a obține corect. Încălcați-le și puteți face tot felul de lucruri nebunești, cum ar fi să dovediți că +1 și -1 sunt egale unul cu celălalt.,

în Schimb, la matematică de bază spatele cum să le combine ne arată un lucru bizar…
4.) e, π și eu sunt toți legați unul de celălalt., Știi că, dacă aveți standard x și y axe (atât reale), puteți, de asemenea, reprezintă coordonatele spațiale prin coordonate polare, în cazul în care aveți un radiale de coordonate (r) și un unghi polar (θ), astfel:
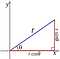
ei Bine, dacă veți crea, în loc de un x și axa y, o reală și imaginară axă, puteți face același lucru, doar că de data asta unghiul θ ia de la avionul real în imaginar avion și înapoi din nou!

Cel mai uimitor lucru despre acest lucru este că, dacă vom naviga la poziția de -1 pe axa reală, ajungem la un frumos identitate:

Nu este: un simplu și neașteptat de legătură între e, i, și π. Aceste relații apar foarte mult în analiza complexă. Și totuși, dacă sunteți dispus să luați în considerare exponențialele, acesta din urmă este un doozy…
5.) i^i, sau am ridicat la puterea i, este 100% real., Gândiți-vă la ecuația din imaginea de mai sus — formula lui Euler-dar în loc să ne îndreptăm spre (-1) pe axa reală, să ne îndreptăm spre i pe axa imaginară.,d=”952eecae59″>
ei Bine, dacă vrem să știm ce i^i este, tot ce trebuie să faceți este să ridice ambele părți ale ecuației la putere,

și amintiți-vă că i^2 = -1, și găsim că:

care este de aproximativ ~0.,20788, un număr pur real. Și acestea sunt primele mele 5 fapte matematice distractive despre numere imaginare!




