« Il n’y a pas assez d’amour et de bonté dans le monde pour permettre de le donner à des êtres imaginaires. »- Friedrich Nietzsche
parfois, si vous voulez décrire l’univers dans lequel vous vivez avec précision, vous devez aller au-delà des modes de pensée conventionnels. Au début du 20e siècle, deux révolutions de la physique — la relativité D’Einstein (d’abord spéciale, puis générale) et la mécanique quantique — ont amené le besoin de mathématiques au-delà de ce que les nombres réels pourraient nous apporter seuls., Depuis, les mathématiques complexes, composées à la fois de parties réelles et imaginaires, sont inextricablement liées à notre compréhension de l’univers.

mathématiquement, lorsque nous pensons aux nombres, nous pouvons penser à quelques façons différentes de les catégoriser:
- Les Nombres dénombrables: 1, 2, 3, 4, etc., Il y a un nombre infini de ces.
- Les nombres entiers: 0, 1, 2, 3, etc. Ce sont les mêmes que les dénombrables, mais ils incluent également zéro.
- Les entiers: …, -3, -2, -1, 0, 1, 2, 3, etc. Cela peut ne pas sembler beaucoup, mais la reconnaissance que nous pouvons avoir des nombres négatifs était énorme, et qu’il peut y en avoir autant de négatifs qu’il y en a de positifs. Cela comprend tous les nombres entiers ainsi que leurs négatifs.
- Les rationnels: tout nombre qui peut être exprimé comme une fraction d’un entier sur un autre., Cela inclut tous les entiers (qui peuvent être exprimés eux-mêmes sur un) ainsi qu’un nombre infini de rationnels entre chaque entier. Toute décimale se répétant à l’infini peut être exprimée comme un nombre rationnel.
- Les réels: comprend tous les rationnels ainsi que tous les nombres irrationnels, tels que les racines carrées des carrés non parfaits, π et une foule d’autres. La somme de tout nombre rationnel et de tout nombre irrationnel sera irrationnelle, mais les sommes de deux irrationnels peuvent être rationnelles.,
Mais, tandis que la racine carrée d’un nombre positif est réel, la racine carrée d’un nombre négatif n’est pas bien définie.

au moins, ce n’était pas le cas, jusqu’à ce que nous les définissions et inventions les nombres imaginaires pour faire exactement cela! Un nombre imaginaire est comme un nombre réel, sauf qu’il est multiplié par” i », ou la racine carrée de (-1)., Les nombres peuvent également être complexes, où ils ont à la fois une partie réelle (a) et une partie imaginaire (b), et sont normalement exprimés en (a + bi).
Maintenant que vous savez ce qu’ils sont, voici mon top 5 des faits amusants sur les nombres imaginaires!
1.) La racine carrée de i A à la fois des parties réelles et imaginaires. La racine carrée d’un nombre réel négatif est purement imaginaire, mais la racine carrée d’un nombre purement imaginaire doit avoir à la fois des parties réelles et imaginaires! Voici comment vous pouvez prouver à vous-même. Vous avez besoin d’un certain nombre, au carré, égal à √(-1)., Imaginez qu’il puisse avoir une partie réelle, x, et une partie imaginaire, y, afin que nous puissions l’écrire comme (x + yi). Puis nous avons pu comprendre ce que x et y doivent être pour que cela fonctionne.,

nous avons donc le carré des deux côtés,

et maintenant, nous correspondre la partie réelle avec la partie réelle, et la partie imaginaire avec la partie imaginaire., nous pouvons résoudre pour y:

Comme vous pouvez le voir, il y a deux solutions possibles, et si l’on utilise la main droite (partie imaginaire) de l’équation à résoudre pour x (qui s’avère égale à y, dans les deux cas), on obtient les deux solutions:

ce Qui nous amène à la prochaine fait amusant…
2.,) Toute racine de i a plusieurs solutions uniques, et la n-th racine a N solutions uniques. Pour les nombres réels positifs, prendre la racine carrée (c’est-à-dire la deuxième racine) de ce nombre vous donne deux solutions possibles: une positive et une négative. Par exemple, √(1) peut être +1, ou il peut être -1, depuis un carré vous donne 1.
Mais j’, ou √(-1), si vous voulez prendre racines de cela, vous devez faire une équation polynomiale, comme nous l’avons fait ci-dessus. Le fait est que l’ordre de l’équation polynomiale dépend de la racine que nous en prenons., Ainsi, le troisième, la quatrième et la cinquième racines de je satisfaire:

Et il y en aura trois, quatre, et cinq de solutions uniques (respectivement) pour chaque x et y dans ces équations., Par exemple, les trois solutions pour le cube (3e) de la racine de i sont:

(Essayez de cubage toutes ces, et de voir par vous-même!) Et cela ne concerne même pas les fractions, qui sont une toute autre boîte de vers. En fait…
3.) Dans une fraction imaginaire, il importe réellement que le numérateur ou le dénominateur ait le « i” dedans., Si vous pensez au nombre (-1), peu importe si vous le pensez, en termes fractionnaires, comme(-1)/1 ou comme 1/(-1); c’est toujours le nombre (-1) de toute façon. Mais ce n’est pas le cas pour moi! Permettez-moi de vous demander ceci: Que pensez-vous de cette fraction?

en Regardant cela, vous pourriez penser qu’il est juste égal à i, mais c’est en réalité-je!
vous Voulez prouver?, Il suffit de multiplier le haut et le bas par i, et voyez par vous-même:

la chose dont vous devez faire très attention est que lorsque vous combinez ou séparez des racines carrées de nombres négatifs, il existe des règles complexes que vous devez suivre pour le corriger. Violez-les, et vous pouvez faire toutes sortes de choses folles, comme prouver que +1 et -1 sont égaux les uns aux autres.,

Au Lieu de cela, les mathématiques sous-jacentes derrière la façon de les combiner nous montrent une chose vraiment bizarre
4.) e, π et i sont tous liés l’un à l’autre., Vous savez que si vous avez votre standard x-et-y des axes (réel), vous pouvez également représenter que des coordonnées de l’espace en coordonnées polaires, où vous avez une coordonnée radiale (r) et un angle polaire (θ), comme ceci:
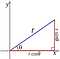
Eh bien, si vous créez, au lieu d’un axe x et y, un axe réel et imaginaire, vous pouvez faire la même chose, sauf que cette fois l’angle θ Vous emmène du plan réel dans le plan imaginaire et retour!

Le plus étonnant, c’est que si nous naviguer jusqu’à la position de -1 sur l’axe réel, nous arrivons à une belle identité:

c’est Là: un simple et inattendu de la relation entre e, i, et pi. Ces relations apparaissent beaucoup dans une analyse complexe. Et pourtant, si vous êtes prêt à considérer les exponentielles, ce dernier est un doozy
5.) I^i, ou j’ai élevé au pouvoir i, est 100% réel., Pensez à l’équation dans l’image ci — dessus — la formule D’Euler-mais au lieu de se diriger vers (-1) sur l’axe réel, dirigons-nous vers i sur l’axe imaginaire à la place.,d= »952eecae59″>
eh Bien, si nous voulons savoir ce que j’ai^i est, tout ce que nous devons faire est de lever les deux côtés de cette équation pour la je de la puissance,

et n’oubliez pas que i^2 = -1, et nous constatons que:

qui est d’environ ~0.,20788, un nombre purement réel. Et ce sont mes 5 meilleurs faits mathématiques amusants sur les nombres imaginaires!




