“There is not enough love and goodness in the world to permit giving any of it away to imaginary beings.”-Friedrich Nietzsche
às Vezes, se você quiser descrever o Universo você vive com precisão, você precisa ir além das formas convencionais de pensar. No início do século XX, duas revoluções na física — a relatividade de Einstein (primeiro especial, depois geral) e a mecânica quântica — trouxeram a necessidade de matemática além do que os números reais poderiam nos trazer sozinhos., Desde então, a matemática complexa, que consiste em partes reais e imaginárias, tem sido intrinsecamente entrelaçada com a nossa compreensão do universo.

Matematicamente, quando pensamos em números, podemos pensar em algumas maneiras diferentes para categorizá-los:
- O contável números: 1, 2, 3, 4, etc., Há um número infinito deles.
- os números inteiros: 0, 1, 2, 3, etc. Estes são os mesmos que os contáveis, mas também incluem zero.os inteiros: …, -3, -2, -1, 0, 1, 2, 3, etc. Pode não parecer muito, mas o reconhecimento de que podemos ter números negativos foi enorme, e que pode haver tantos negativos quanto positivos. Isto inclui todos os números inteiros, bem como seus negativos.
- The rations: any number that can be expressed as a fraction of one integer over another., Isto inclui todos os inteiros (que podem ser expressos como eles mesmos sobre um), bem como um número infinito de racionais entre cada inteiro. Qualquer decimal infinitamente repetitivo pode ser expresso como um número racional.
- os reais: inclui todos os Racionais, bem como todos os números irracionais, tais como as raízes quadradas de quadrados não-perfeitos, π, e uma série inteira de outros. A soma de qualquer número racional e qualquer número irracional será irracional, mas as somas de duas irracionais podem ser racionais.,
mas, enquanto a raiz quadrada de um número positivo é real, a raiz quadrada de um número negativo não está bem definida.

Pelo menos, não era, até que nós definimos, e inventou os números imaginários para fazer exatamente isso! Um número imaginário é exatamente como um real, exceto que é multiplicado por” i”, ou a raiz quadrada de (-1)., Os números também podem ser complexos, onde eles têm uma parte real (a) e uma parte imaginária (B), e são normalmente expressos como (a + bi).agora que sabe o que são, aqui estão os meus cinco melhores factos sobre números imaginários!1.) A raiz quadrada de i tem partes reais e imaginárias. A raiz quadrada de um número real negativo é puramente imaginária, mas a raiz quadrada de um número puramente imaginário tem de ter partes tanto reais como imaginárias! Eis como podes prová-lo a ti próprio. Você precisa de algum Número, ao quadrado, para igual √(-1)., Imagine que poderia ter uma parte real, x, e uma parte imaginária, y, para que pudéssemos escrevê-la como (x + yi). Depois podemos descobrir o que x e y precisam de ser para isto funcionar.,

então, nós quadrado ambos os lados,

e agora nós igualar-se a parte real com a parte real, e a parte imaginária com a parte imaginária.,, podemos resolver para y:

Como você pode ver, existem duas soluções possíveis, e se usamos a mão direita (parte imaginária) da equação para resolver o x (que acaba de igualdade de y em ambos os casos), temos duas soluções:

o Que nos leva ao seguinte fato engraçado…
2.,) Qualquer raiz de i tem múltiplas soluções únicas, e a n-ésima raiz tem n soluções únicas. Para números positivos, reais, tomando a raiz quadrada (isto é, a segunda raiz) desse número dá-lhe duas soluções possíveis: uma positiva e uma negativa. Por exemplo, √(1) pode ser +1, ou pode ser -1, uma vez que qualquer um ao quadrado lhe dará 1.
But for i, or √(-1), if you want to take roots of that, you have to make a polynomial equation, like we did above. A coisa é, a ordem da equação polinomial é dependente de que raiz nós tomamos dela., Então, o terceiro, quarto e quinto raízes de eu ter que satisfazer:

E haverá três, quatro, e cinco soluções únicas (respectivamente) para cada x e y nessas equações., Por exemplo, as três soluções para o cubed (3) raiz do eu são:

(Tente cubagem de todos estes, e veja por si mesmo!) E isso nem sequer é lidar com frações, que são uma outra lata inteira de vermes. De facto…
3. Em uma fração imaginária, ele realmente importa se o numerador ou denominador tem o ” i ” nela., Se você pensar no número (-1), não importa se você pensa nele, em termos fracionais, como (-1)/1 ou como 1/(-1); ainda é o número (-1) de qualquer maneira. Mas não é esse o caso para mim! Deixa-me perguntar-te isto: o que achas que é esta fracção?

a Olhar para ele, você pode pensar que é apenas igual a eu, mas na verdade -eu!queres prová-lo?, Basta multiplicar superior e inferior por eu, e veja por si mesmo:

A única coisa que você tem que ter muito cuidado é que quando você combinar ou separar as raízes quadradas de números negativos, não são intrincadas regras que você deve seguir para obtê-lo correto. Violá-los, e você pode fazer todo o tipo de coisas insanas, como provar que +1 e -1 são iguais um ao outro.,

em vez disso, a matemática subjacente por trás de como combiná-los mostra-nos uma coisa realmente bizarra…
4.) e, π, And I are all related to one another., Você sabe que se você tem o seu padrão de x-e-y eixos (real), você pode também representar esse espaço coordenado por coordenadas polares, onde você tem uma coordenada radial (r) e um ângulo polar (θ), assim:
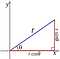
Bem, se você criar, em vez de um x-e-y eixo real e o eixo imaginário, você pode fazer a mesma coisa, exceto que desta vez o ângulo θ leva você a partir do plano real em um plano imaginário e de volta outra vez!

A coisa surpreendente sobre isso é que, se nós navegar para a posição de -1 no eixo real, chegamos a uma bela identidade:

Não é: um simples e inesperada, uma relação entre a e, i, e π. Estas relações aparecem muito em análises complexas. E ainda assim, se você está disposto a considerar exponenciais, este último é um doozy …
5.) i^i, ou I elevado ao poder i, é 100% real., Pense sobre a equação na imagem acima-a fórmula de Euler-mas em vez de ir para (-1) no eixo real, vamos dirigir-nos para i no eixo imaginário em vez disso.,d=”952eecae59″>
Bem, se queremos saber o que eu^i é, tudo o que precisamos fazer é aumentar em ambos os lados desta equação para o poder,

e lembre-se de que i^2 = -1, e descobrimos que:

, que é de cerca de ~0.,20788, um número puramente real. E esses são os meus cinco melhores factos matemáticos sobre números imaginários!




