Come faccio a sapere quando utilizzare il t-test invece di z-test?
Quasi ogni studente di statistica che abbia mai insegnato mi ha chiesto questo domanda ad un certo punto., Quando ho iniziato il tutoraggio, spiegavo che dipende dal problema e iniziavo a vagare sul teorema del limite centrale fino a quando i loro occhi non si illuminavano. Poi ho capito, è più facile capire se faccio solo un diagramma di flusso. Quindi, eccolo qui!
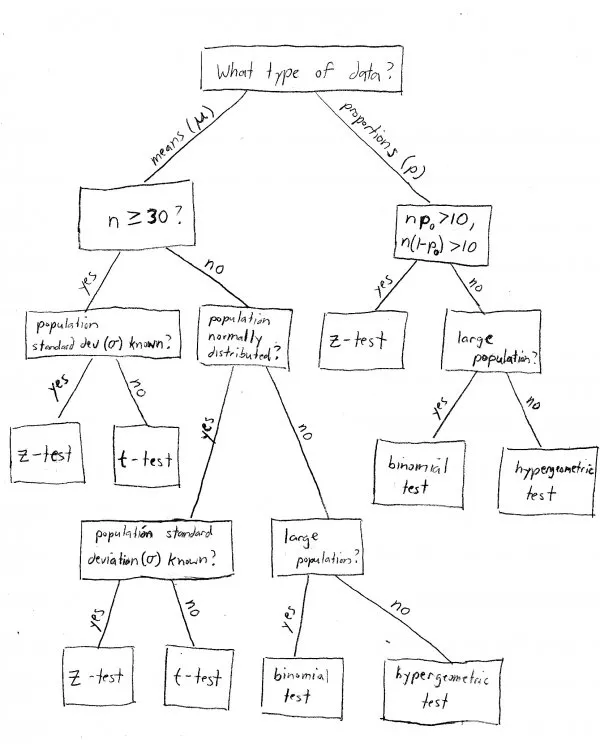
Fondamentalmente, dipende da quattro cose:
- Se stiamo lavorando con una media (ad esempio, “37 studenti”) o una proporzione (ad esempio, “15% di tutti gli studenti”).
- Se conosciamo o meno la deviazione standard della popolazione (\(\sigma\))., Nella vita reale di solito non lo facciamo, ma i corsi di statistica amano escogitare problemi dove lo facciamo.
- Se la popolazione è normalmente distribuita. Questo è importante soprattutto quando si tratta di campioni di piccole dimensioni.
- La dimensione del nostro campione. Il numero magico è di solito 30-sotto che è considerato un campione “piccolo”, e 30 o superiore è considerato”grande”. Quando la dimensione del campione è grande, il teorema del limite centrale ci dice che non dobbiamo preoccuparci se la popolazione è normalmente distribuita.,
In generale, il problema ti dirà esplicitamente se la deviazione standard della popolazione è nota – se non lo dicono, supponiamo che sia sconosciuta. Lo stesso vale per una popolazione normalmente distribuita – se non dicono “supponiamo che la popolazione sia normalmente distribuita”, o qualcosa del genere, allora non fare solo questa ipotesi. Fortunatamente se la dimensione del campione è abbastanza grande, non importa!
Inizia con un tutor di statistiche a IU oggi!




