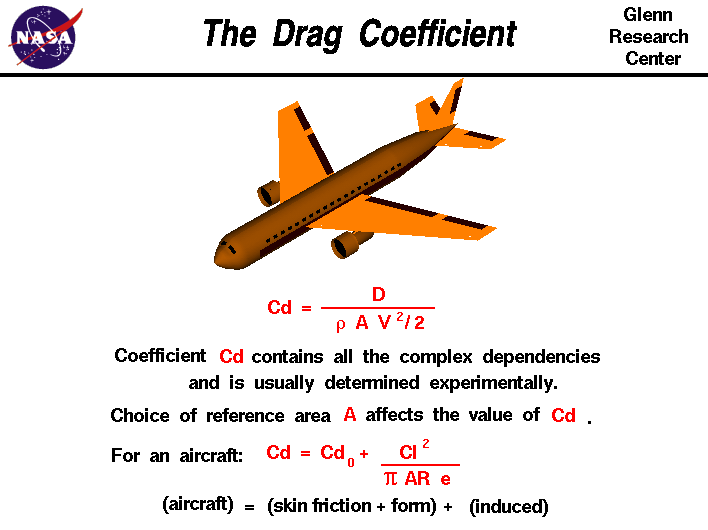
Il Coefficiente di resistenza

Il coefficiente di resistenza è un numero che aerodynamicists utilizzare per modelall del complesso dipendenze di forma,inclinazione, e le condizioni di flusso su aircraftdrag.Questa equazione è semplicemente una disposizione dell’equazione di trascinamento in cui risolviamo il coefficiente di trascinamento in termini di altre variabili.Il coefficiente di resistenza Cd è uguale alla resistenza D diviso per la quantità: densità r timeshalf la velocità V al quadrato per l’area di riferimento A.,

La quantità della metà della densità di volte la velocità al quadrato è chiamato thedynamic pressione q. Così

Il coefficiente di trascinamento esprime quindi theratioof la forza di resistenza alla forza generata dalla pressione dinamica volte l’area.

Questa equazione ci dà un modo per determinare un valore per il dragcoefficient. In un ambiente controllato (windtunnel) possiamo impostare la velocità, la densità e l’area e misurare la resistenza prodotta., Attraverso la divisione arriviamo a un valore per il dragcoefficient. Come sottolineato sulla diapositiva dragequation, la scelta di referencearea (area alare, area frontale, superficie, …) influenzerà il valore numerico effettivo del coefficiente di resistenza calcolato.Quando si riportano i valori del coefficiente di resistenza, è importante specificarel’area di riferimento utilizzata per determinare il coefficiente. Noi canpredict il trascinamento che sarà prodotto sotto un ofvelocity di serie diverso, densità (altitudine), e condizioni di area usando l’equazione di trascinamento.,

Il coefficiente di resistenza contiene non solo le dipendenze complesse di forma e inclinazione dell’oggetto, ma anche gli effetti di airviscosity e compressibilità. Per utilizzare correttamente il dragcoefficient, dobbiamo essere sicuri che la viscosità e la compressibilityeffects siano gli stessi tra il nostro caso misurato e il predictedcase. Altrimenti, la previsione sarà imprecisa. Per velocità molto basse (< 200 mph) gli effetti di compressibilità sono trascurabili. Athigher velocità, diventa importante abbinare i numeri di Mach tra thetwo casi.,Il numero di mach è il rapporto tra la velocità e la velocità di sound.At velocità supersoniche, onde d’urto saranno presenti nel campo di flusso e dobbiamo essere sicuri di tenere conto del coefficiente di trascinamento dell’onda. Quindi è completamente errato misurare un dragcoefficient a bassa velocità (diciamo 200 mph) e applicare quel dragcoefficient al doppio della velocità del suono (circa 1.400 mph,Mach = 2.0). È ancora più importante abbinare la viscosità dell’ariaeffetti. L’importante parametro di corrispondenza per la viscosità è ilnoldi numeroche esprime il rapporto tra forze inerziali e forze viscose., Nelle nostre discussioni sulle fonti di resistenza,ricordiamo che la resistenza all’attrito della pelle dipende direttamente dall’interazione viscosa dell’oggetto e del flusso. Se il numero di Reynolds dell’esperimento e del volo sono vicini, allora modelliamo correttamente gli effetti delle forze viscose rispetto alle forze inerziali. Se sono molto diversi, non modelliamo correttamente la fisica del problema reale e prevediamo un trascinamento errato.

L’equazione del coefficiente di resistenza si applica a qualsiasi oggetto se corrispondiamo correttamente alle condizioni di flusso., Se stiamo considerando un aeromobile, possiamopensare al coefficiente di resistenza come composto da due componenti principali; un coefficiente di resistenza di base che include gli effetti dell’attrito della pelle e della forma (forma) e un coefficiente di resistenza aggiuntivo relativo al sollevamento dell’aeromobile.Questa fonte aggiuntiva di trascinamento è chiamata dragor trascinamento indotto a causa del sollevamento. La resistenza indotta si verifica a causa della distribuzione del sollevamento attraverso l’arco dell’ala. A causa delle differenze di pressione sopra e sotto l’ala, l’aria sul fondo dell’ala è disegnata sulla parte superiore vicino alle punte delle ali., Questo crea un flusso vorticosoche cambia l’angolo efficace di attacco lungo l’ala e “induce”una resistenza sull’ala. La resistenza indotta coefficiente di Cdi è uguale al quadrato del coefficiente di portanza Cl diviso per la quantità: pi(3.14159) volte il rapporto di aspetto AR volte anefficiency fattore e.

Il rapporto di aspetto è il quadrato di thespan s diviso per la superficie alare A.,

Per un’ala rettangolare questo si riduce al rapporto tra la campata e la corda.Le ali lunghe, snelle e ad alto rapporto di aspetto hanno una minore resistenza indotta rispetto alle ali corte, spesse e a basso rapporto di aspetto. La teoria della linea di sollevamento mostra che la resistenza indotta ottimale (più bassa) si verifica per una distribuzione ellittica di sollevamento da punta a punta. Il fattore di efficienza e è uguale a 1,0 per una distribuzione ellittica ed è un valore inferiore a 1,0 per qualsiasi altra distribuzione di sollevamento. Un valore tipico per e per un ala rettangolare è .70 ., Le prestazioni aerodinamiche eccezionali dello Spitfire britannico della seconda guerra mondiale sono parzialmente attribuibili alla sua ala a forma ellittica che ha dato all’aereo una quantità molto bassa di resistenza indotta.Il coefficiente totaldrag Cd è uguale al coefficiente di resistenza a zero ascensore Cdoplus il coefficiente di resistenza indotta Cdi.

Il coefficiente di resistenza in questa equazione utilizza l’area alare per l’area di riferimento. Altrimenti, non potremmo aggiungerlo alquadrato del coefficiente di sollevamento, che si basa anche sulla wingarea.,> Activities:
Guided Tours

• Drag Equation:
• Sources of Drag:
• Factors that Affect Drag:
• Wind Tunnels:
• Forces on a Model Rocket:

Navigation .,.

Beginner’s Guide Home Page