Obiettivi formativi
Alla fine di questa sezione, sarete in grado di:
- Descrivere l’azione di un condensatore e definire la capacità.
- Spiegare i condensatori a piastre parallele e le loro capacità.
- Discutere il processo di aumento della capacità di un dielettrico.
- Determinare capacità dato carica e tensione.
Un condensatore è un dispositivo utilizzato per memorizzare carica elettrica., I condensatori hanno applicazioni che vanno dal filtraggio statico della ricezione radio allo stoccaggio di energia nei defibrillatori cardiaci. In genere, i condensatori commerciali hanno due parti di conduzione vicine l’una all’altra, ma non toccanti, come quelle in Figura 1. (La maggior parte delle volte viene utilizzato un isolante tra le due piastre per fornire la separazione—vedere la discussione sui dielettrici di seguito.) Quando i terminali della batteria sono collegati a un condensatore inizialmente non caricato, quantità uguali di carica positiva e negativa, +Q e –Q, sono separate nelle sue due piastre., Il condensatore rimane neutro nel complesso, ma ci riferiamo ad esso come memorizzazione di una carica Q in questa circostanza.

Figura 1. Entrambi i condensatori mostrati qui sono stati inizialmente scaricati prima di essere collegati a una batteria. Ora hanno separato le cariche di + Q e-Q sulle loro due metà. (a) Un condensatore a piastra parallela. b) Un condensatore laminato con un materiale isolante tra i suoi due fogli conduttori.
Condensatore
Un condensatore è un dispositivo utilizzato per memorizzare carica elettrica.,
La quantità di carica Q un condensatore può memorizzare dipende da due fattori principali—la tensione applicata e le caratteristiche fisiche del condensatore, come la sua dimensione.
La quantità di carica Q un condensatore può memorizzare
La quantità di carica Q un condensatore può memorizzare dipende da due fattori principali-la tensione applicata e le caratteristiche fisiche del condensatore, come ad esempio la sua dimensione.

Figura 2. Le linee di campo elettrico in questo condensatore a piastra parallela, come sempre, iniziano con cariche positive e terminano con cariche negative., Poiché l’intensità del campo elettrico è proporzionale alla densità delle linee di campo, è anche proporzionale alla quantità di carica sul condensatore.
Un sistema composto da due piastre di conduzione parallele identiche separate da una distanza, come in Figura 2, è chiamato condensatore a piastra parallela. È facile vedere la relazione tra la tensione e la carica memorizzata per un condensatore a piastra parallela, come mostrato in Figura 2. Ogni linea di campo elettrico inizia con una singola carica positiva e termina con una negativa, in modo che ci saranno più linee di campo se c’è più carica., (Disegnare una singola linea di campo per carica è solo una comodità. Possiamo disegnare molte linee di campo per ogni carica, ma il numero totale è proporzionale al numero di cariche.) L’intensità del campo elettrico è, quindi, direttamente proporzionale a Q.
Il campo è proporzionale alla carica:
E Q Q,
dove il simbolo∝significa “proporzionale a.”Dalla discussione sul potenziale elettrico in un campo elettrico uniforme, sappiamo che la tensione attraverso le piastre parallele è
V = Ed.
Quindi, V E E., Ne consegue, quindi, che V Q Q, e viceversa,
Q V V.
Questo è vero in generale: maggiore è la tensione applicata a qualsiasi condensatore, maggiore è la carica memorizzata in esso.
Diversi condensatori memorizzeranno diverse quantità di carica per la stessa tensione applicata, a seconda delle loro caratteristiche fisiche. Definiamo la loro capacità C tale che la carica Q immagazzinata in un condensatore sia proporzionale a C. La carica immagazzinata in un condensatore è data da
Q = CV.,
Questa equazione esprime i due principali fattori che influenzano la quantità di carica memorizzata. Questi fattori sono le caratteristiche fisiche del condensatore, C, e la tensione, V. Riorganizzando l’equazione, vediamo che la capacità C è la quantità di carica memorizzata per volt, o
C = \ frac {Q} {V}\\.,
Capacità
Capacità C è la quantità di carica immagazzinata per volt, o
C=\frac{Q}{V}\\
L’unità della capacità è il farad (F), denominato per Michael Faraday (1791-1867), uno scienziato inglese che ha contribuito ai campi di elettromagnetismo e dell’elettrochimica. Poiché la capacità è carica per unità di tensione, vediamo che un farad è un coulomb per volt, o
1\text{ F}=\frac{1\text{ C}}{1\text{ V}}\\.,
Un condensatore 1-farad sarebbe in grado di memorizzare 1 coulomb (una quantità molto grande di carica) con l’applicazione di solo 1 volt. Un farad è, quindi, una capacità molto grande. I condensatori tipici vanno da frazioni di picofarad (1 pF = 10-12 F) a millifarad (1 mF = 10-3 F).
La figura 3 mostra alcuni condensatori comuni. I condensatori sono realizzati principalmente in ceramica, vetro o plastica, a seconda dello scopo e delle dimensioni. I materiali isolanti, chiamati dielettrici, sono comunemente usati nella loro costruzione, come discusso di seguito.

Figura 3., Alcuni condensatori tipici. La dimensione e il valore della capacità non sono necessariamente correlati. (credito: Windell Oskay)
Condensatore a piastra parallela

Figura 4. Condensatore a piastra parallela con piastre separate da una distanza d. Ogni piastra ha un’area A.
Il condensatore a piastra parallela mostrato in Figura 4 ha due piastre di conduzione identiche, ciascuna avente una superficie A, separata da una distanza d (senza materiale tra le piastre). Quando una tensione V viene applicata al condensatore, memorizza una carica Q, come mostrato., Possiamo vedere come la sua capacità dipende da A e d considerando le caratteristiche della forza di Coulomb. Sappiamo che come le cariche respingono, a differenza delle cariche attraggono, e la forza tra le cariche diminuisce con la distanza. Quindi sembra abbastanza ragionevole che più grandi sono le piastre, più carica possono memorizzare—perché le cariche possono diffondersi di più. Quindi C dovrebbe essere maggiore per il più grande A. Allo stesso modo, più le piastre sono vicine, maggiore è l’attrazione delle cariche opposte su di esse. Quindi C dovrebbe essere maggiore per d più piccolo.,
Si può dimostrare che per un condensatore a piastra parallela ci sono solo due fattori (A e d) che influenzano la sua capacità C. La capacità di un condensatore a piastra parallela in forma di equazione è data da
C=\epsilon_{o}\frac{A}{d}\\.
Capacità di un condensatore a piastra parallela
C=\epsilon_{o}\frac{A}{d}\\
A è l’area di una piastra in metri quadrati e d è la distanza tra le piastre in metri. La costante ε0 è la permittività dello spazio libero; il suo valore numerico in unità SI è ε0 = 8,85 × 10-12 F / m., Le unità di F / m sono equivalenti a C2 / N * m2. Il piccolo valore numerico di ε0 è correlato alle grandi dimensioni del farad. Un condensatore a piastra parallela deve avere una vasta area per avere una capacità che si avvicina a un farad. (Si noti che l’equazione di cui sopra è valida quando le piastre parallele sono separate da aria o spazio libero. Quando un altro materiale viene posizionato tra le piastre, l’equazione viene modificata, come discusso di seguito.)
Un altro interessante esempio biologico che si occupa di potenziale elettrico si trova nella membrana plasmatica della cellula., La membrana imposta una cellula fuori dall’ambiente circostante e permette anche agli ioni di passare selettivamente dentro e fuori dalla cellula. C’è una differenza di potenziale attraverso la membrana di circa -70 mV . Ciò è dovuto principalmente agli ioni caricati negativamente nella cellula e alla predominanza di ioni di sodio caricati positivamente (Na+) all’esterno. Le cose cambiano quando una cellula nervosa viene stimolata. Gli ioni Na + possono passare attraverso la membrana nella cellula, producendo un potenziale di membrana positivo—il segnale nervoso. La membrana cellulare ha uno spessore di circa 7-10 nm., Un valore approssimativo del campo elettrico attraverso di esso è dato da
\displaystyle{E}=\frac{V}{d}=\frac{-70\times10^{-3}\text{ V}}{8\times10^{-9}\text{ m}}=-9\times10^{6}\text{ V/m}\\
Questo campo elettrico è sufficiente a causare una rottura in aria.
Dielettrico
L’esempio precedente evidenzia la difficoltà di immagazzinare una grande quantità di carica nei condensatori. Se d viene ridotto per produrre una capacità maggiore, la tensione massima deve essere ridotta proporzionalmente per evitare la rottura (poiché E= \ frac{V} {d}\\)., Una soluzione importante a questa difficoltà è mettere un materiale isolante, chiamato dielettrico, tra le piastre di un condensatore e consentire a d di essere il più piccolo possibile. Non solo la d più piccola rende la capacità maggiore, ma molti isolanti possono sopportare campi elettrici maggiori dell’aria prima di rompersi.
I valori della costante dielettrica κ per vari materiali sono riportati nella Tabella 1. Si noti che κ per il vuoto è esattamente 1, e quindi l’equazione precedente è valida anche in questo caso., Se si utilizza un dielettrico, magari posizionando Teflon tra le piastre del condensatore nell’esempio 1, allora la capacità è maggiore del fattore κ, che per Teflon è 2.1.
Take-Home Experiment: Costruire un condensatore
Quanto è grande un condensatore si può fare con un involucro di gomma da masticare? Le piastre saranno il foglio di alluminio e la separazione (dielettrica) in mezzo sarà la carta.
| Tabella 1., Dielectric Constants and Dielectric Strengths for Various Materials at 20ºC | ||
|---|---|---|
| Material | Dielectric constant κ | Dielectric strength (V/m) |
| Vacuum | 1.00000 | — |
| Air | 1.00059 | 3 × 106 |
| Bakelite | 4.9 | 24 × 106 |
| Fused quartz | 3.78 | 8 × 106 |
| Neoprene rubber | 6.7 | 12 × 106 |
| Nylon | 3.,4 | 14 × 106 |
| Paper | 3.7 | 16 × 106 |
| Polystyrene | 2.56 | 24 × 106 |
| Pyrex glass | 5.6 | 14 × 106 |
| Silicon oil | 2.5 | 15 × 106 |
| Strontium titanate | 233 | 8 × 106 |
| Teflon | 2.,1 | 60 × 106 |
| Acqua | 80 | — |
si noti, inoltre, che la costante dielettrica per aria è molto vicino a 1, in modo che l’aria condensatori riempiti con atto molto simili a quelle con il vuoto tra loro piatti, tranne che l’aria può diventare conduttivo se l’intensità di campo elettrico diventa troppo grande. (Ricordiamo che E = \ frac{V} {d} \ \ per un condensatore a piastra parallela.) Anche mostrato nella Tabella 1 sono massime intensità di campo elettrico in V / m, chiamati resistenze dielettriche, per diversi materiali., Questi sono i campi sopra i quali il materiale inizia a rompersi e condurre. La rigidità dielettrica impone un limite alla tensione che può essere applicata per una determinata separazione della piastra. Ad esempio, nell’esempio 1, la separazione è di 1,00 mm, e quindi il limite di tensione per l’aria è
Tuttavia, il limite per una separazione di 1,00 mm riempita con Teflon è 60.000 V, poiché la rigidità dielettrica del Teflon è 60 × 106 V/m. Quindi lo stesso condensatore riempito con Teflon ha una capacità maggiore e può essere sottoposto a una tensione molto maggiore., Using the capacitance we calculated in the above example for the air-filled parallel plate capacitor, we find that the Teflon-filled capacitor can store a maximum charge of
\begin{array}{lll}Q&=&CV\\\text{ }&=&\kappa{C}_{\text{air}}V\\\text{ }&=&(2.1)(8.85\text{ nF})(6.0\times10^4\text{ V})\\\text{ }&=&1.,1 \ text {mC} \ end {array} \ \
Questo è 42 volte la carica dello stesso condensatore riempito d’aria.
Rigidità dielettrica
La massima intensità del campo elettrico al di sopra della quale un materiale isolante inizia a rompersi e a condurre è chiamata rigidità dielettrica.
Microscopicamente, in che modo un dielettrico aumenta la capacità? La polarizzazione dell’isolante è responsabile. Più facilmente è polarizzato, maggiore è la sua costante dielettrica κ., L’acqua, ad esempio, è una molecola polare perché un’estremità della molecola ha una leggera carica positiva e l’altra estremità ha una leggera carica negativa. La polarità dell’acqua fa sì che abbia una costante dielettrica relativamente grande di 80. L’effetto della polarizzazione può essere meglio spiegato in termini di caratteristiche della forza di Coulomb. La figura 5 mostra schematicamente la separazione della carica nelle molecole di un materiale dielettrico posto tra le piastre cariche di un condensatore., La forza di Coulomb tra le estremità più vicine delle molecole e la carica sulle piastre è attraente e molto forte, poiché sono molto vicine tra loro. Questo attira più carica sulle piastre che se lo spazio fosse vuoto e le cariche opposte fossero a una distanza d di distanza.

Figura 5. (a) Le molecole nel materiale isolante tra le piastre di un condensatore sono polarizzate dalle piastre caricate., Questo produce uno strato di carica opposta sulla superficie del dielettrico che attira più carica sulla piastra, aumentando la sua capacità. (b) Il dielettrico riduce l’intensità del campo elettrico all’interno del condensatore, con conseguente minore tensione tra le piastre per la stessa carica. Il condensatore memorizza la stessa carica per una tensione più piccola, il che implica che ha una capacità maggiore a causa del dielettrico.
Un altro modo per capire come un dielettrico aumenta la capacità è considerare il suo effetto sul campo elettrico all’interno del condensatore., La figura 5 (b) mostra le linee di campo elettrico con un dielettrico in posizione. Poiché le linee di campo terminano con cariche nel dielettrico, ce ne sono meno che vanno da un lato all’altro del condensatore. Quindi l’intensità del campo elettrico è inferiore se ci fosse un vuoto tra le piastre, anche se la stessa carica è sulle piastre. La tensione tra le piastre è V = Ed, quindi anch’essa è ridotta dal dielettrico. Quindi c’è una tensione V più piccola per la stessa carica Q; poiché C=\frac{Q}{V}\\, la capacità C è maggiore.,
La costante dielettrica è generalmente definita come \kappa=\frac{E_0}{E}\\, o il rapporto tra il campo elettrico nel vuoto e quello nel materiale dielettrico, ed è intimamente correlato alla polarizzabilità del materiale.
Cose grandi e piccole: L’origine submicroscopica della polarizzazione
La polarizzazione è una separazione di carica all’interno di un atomo o molecola. Come è stato notato, il modello planetario dell’atomo lo raffigura come avente un nucleo positivo orbitato da elettroni negativi, analogo ai pianeti orbitanti attorno al Sole., Sebbene questo modello non sia completamente accurato, è molto utile per spiegare una vasta gamma di fenomeni e sarà perfezionato altrove, come nella Fisica atomica. L’origine submicroscopica della polarizzazione può essere modellata come mostrato in Figura 6.

Figura 6. La concezione dell’artista di un atomo polarizzato. Le orbite degli elettroni attorno al nucleo sono leggermente spostate dalle cariche esterne (mostrate esagerate). La separazione risultante di carica all’interno dell’atomo significa che è polarizzata., Si noti che la carica a differenza è ora più vicina alle cariche esterne, causando la polarizzazione.
Troveremo nella Fisica atomica che le orbite degli elettroni sono più propriamente viste come nubi di elettroni con la densità della nube correlata alla probabilità di trovare un elettrone in quella posizione (al contrario delle posizioni e dei percorsi definiti dei pianeti nelle loro orbite attorno al Sole). Questa nube è spostata dalla forza di Coulomb in modo che l’atomo in media abbia una separazione di carica., Sebbene l’atomo rimanga neutro, ora può essere la fonte di una forza di Coulomb, poiché una carica portata vicino all’atomo sarà più vicina a un tipo di carica rispetto all’altra.
Alcune molecole, come quelle dell’acqua, hanno una separazione intrinseca di carica e sono quindi chiamate molecole polari. La figura 7 illustra la separazione della carica in una molecola d’acqua, che ha due atomi di idrogeno e un atomo di ossigeno (H2O). La molecola d’acqua non è simmetrica: gli atomi di idrogeno vengono respinti da un lato, dando alla molecola una forma boomerang., Gli elettroni in una molecola d’acqua sono più concentrati attorno al nucleo di ossigeno più altamente carico rispetto ai nuclei di idrogeno. Ciò rende l’estremità dell’ossigeno della molecola leggermente negativa e lascia le estremità dell’idrogeno leggermente positive. La separazione intrinseca della carica nelle molecole polari rende più facile allinearle con campi e cariche esterne. Le molecole polari presentano quindi maggiori effetti di polarizzazione e hanno maggiori costanti dielettriche. Coloro che studiano la chimica scopriranno che la natura polare dell’acqua ha molti effetti., Ad esempio, le molecole d’acqua raccolgono gli ioni molto più efficacemente perché hanno un campo elettrico e una separazione di carica per attirare cariche di entrambi i segni. Inoltre, come evidenziato nel capitolo precedente, l’acqua polare fornisce uno scudo o uno screening dei campi elettrici nelle molecole altamente cariche di interesse nei sistemi biologici.

Figura 7. Concezione dell’artista di una molecola d’acqua. C’è una separazione intrinseca di carica, e quindi l’acqua è una molecola polare., Gli elettroni nella molecola sono attratti dal nucleo dell’ossigeno e lasciano un eccesso di carica positiva vicino ai due nuclei di idrogeno. (Si noti che lo schema a destra è un’illustrazione approssimativa della distribuzione degli elettroni nella molecola d’acqua. Non mostra il numero effettivo di protoni ed elettroni coinvolti nella struttura.)
PhET Explorations: Capacitor Lab
Esplora come funziona un condensatore! Modificare la dimensione delle piastre e aggiungere un dielettrico per vedere l’effetto sulla capacità. Cambiare la tensione e vedere le cariche accumulate sulle piastre., Osservare il campo elettrico nel condensatore. Misurare la tensione e il campo elettrico.
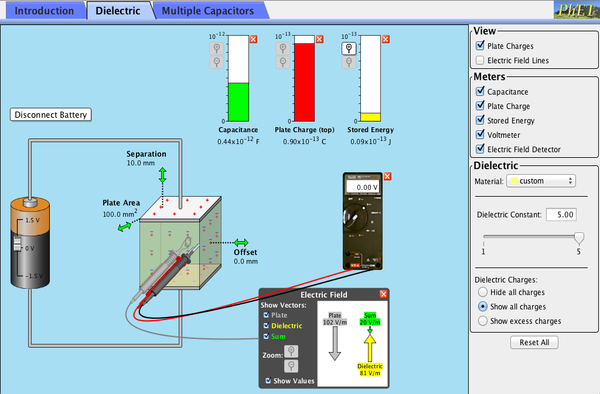
Fare clic per scaricare la simulazione. Esegui usando Java.
Riepilogo della sezione
Domande concettuali
- La capacità di un dispositivo dipende dalla tensione applicata? Che dire della carica memorizzata in esso?
- Usa le caratteristiche della forza di Coulomb per spiegare perché la capacità dovrebbe essere proporzionale all’area della piastra di un condensatore., Allo stesso modo, spiega perché la capacità dovrebbe essere inversamente proporzionale alla separazione tra le piastre.
- Dare il motivo per cui un materiale dielettrico aumenta la capacità rispetto a quello che sarebbe con l’aria tra le piastre di un condensatore. Qual è la ragione indipendente per cui un materiale dielettrico consente anche di applicare una tensione maggiore a un condensatore? (Il dielettrico aumenta quindi C e consente una maggiore V.)
- In che modo il carattere polare delle molecole d’acqua aiuta a spiegare la costante dielettrica relativamente grande dell’acqua? (Vedi Figura 7.,)
- Scintille si verificano tra le piastre di un condensatore riempito d’aria a tensione inferiore quando l’aria è umida rispetto a quando asciutto. Spiega perché, considerando il carattere polare delle molecole d’acqua.
- L’acqua ha una grande costante dielettrica, ma è raramente utilizzata nei condensatori. Spiega perché.
- Le membrane nelle cellule viventi, comprese quelle negli esseri umani, sono caratterizzate da una separazione di carica attraverso la membrana. In effetti, le membrane sono quindi condensatori carichi con importanti funzioni legate alla differenza di potenziale attraverso la membrana., L’energia è necessaria per separare queste cariche nelle membrane viventi e, in tal caso, la sua fonte è la metabolizzazione dell’energia alimentare o qualche altra fonte?

Figura 8. La membrana semipermeabile di una cellula ha diverse concentrazioni di ioni dentro e fuori. La diffusione sposta gli ioni K+ (potassio) e Cl– (cloruro) nelle direzioni mostrate, fino a quando la forza di Coulomb interrompe ulteriormente il trasferimento. Ciò si traduce in uno strato di carica positiva all’esterno, uno strato di carica negativa all’interno e quindi una tensione attraverso la membrana cellulare., La membrana è normalmente impermeabile a Na + (ioni sodio).
Problemi& Esercizi
- Quale carica viene memorizzata in un condensatore da 180 µF quando viene applicato 120 V?
- Trova la carica memorizzata quando 5.50 V viene applicato a un condensatore 8.00 pF.
- Quale carica è memorizzata nel condensatore nell’esempio 1?
- Calcola la tensione applicata a un condensatore da 2,00 µF quando contiene 3,10 µC di carica.
- Quale tensione deve essere applicata a un condensatore 8.00 nF per memorizzare 0.160 mC di carica?
- Che capacità è necessaria per memorizzare 3.,00 µC di carica ad una tensione di 120 V?
- Qual è la capacità di un grande terminale del generatore Van de Graaff, dato che memorizza 8.00 mC di carica ad una tensione di 12.0 MV?
- Trova la capacità di un condensatore a piastra parallela con piastre di area 5,00 m2 separate da 0,100 mm di Teflon.
- (a)Qual è la capacità di un condensatore a piastre parallele con piastre di area 1,50 m2 separate da 0,0200 mm di gomma neoprene? (b) Quale carica tiene quando gli viene applicata 9,00 V?
- Concetti integrati. Un burlone applica 450 V a un 80.,Condensatore 0 µF e poi lo lancia a una vittima ignara. Il dito della vittima viene bruciato dallo scarico del condensatore attraverso 0,200 g di carne. Qual è l’aumento della temperatura della carne? È ragionevole presumere nessun cambiamento di fase?
- Risultati irragionevoli. (a) Un certo condensatore a piastra parallela ha piastre di area 4,00 m2, separate da 0,0100 mm di nylon e memorizza 0,170 C di carica. Qual è la tensione applicata? (b) Cosa c’è di irragionevole in questo risultato? (c) Quali ipotesi sono responsabili o incoerenti?,
Glossario
condensatore: un dispositivo che memorizza carica elettrica
capacità: quantità di carica immagazzinata per unità di volt
dielettrico: un materiale isolante
resistenza dielettrica: il massimo del campo elettrico al di sopra della quale un materiale isolante comincia a crollare e condotta
parallelo piastra condensatore: due identici deflettori, separati da una distanza
molecola polare: una molecola con le inerenti la separazione di carica




