qu’est Ce qu’une phrase?
une phrase numérique est un arrangement de nombres et de symboles, comme le suivant:
6 + 7 = 13
45 – 6 = 39
8 x 9 = 72
48 ÷ 8 = 6
il fut un temps où les enseignants se référaient au mot « somme » lorsqu’ils utilisaient l’un des éléments ci-dessus, mais cela prête à confusion pour les enfants, car le mot « somme » est un terme qui ne devrait être utilisé que lorsqu’on parle d’addition.,
Les enfants commencent à apprendre à écrire des phrases de nombres d’addition et de soustraction en année 1. Ils commenceront probablement à apprendre l’addition en faisant deux groupes (par exemple: 5 bananes et 2 pommes) et en les assemblant. Ils développent ensuite vers la façon d’écrire ces nombres et de les organiser avec les symboles + et = pour faire une phrase numérique qui a du sens.
en année 2, les enfants commencent à écrire des phrases numériques pour la multiplication et la division, ils doivent donc comprendre les symboles: x et ÷ et pouvoir les écrire.,

travailler avec des phrases numériques en classe
à tout moment au stade clé 1 ou 2, les enseignants peuvent montrer aux enfants un problème de mot, puis leur demander d’écrire la phrase numérique qui va avec, par exemple:
j’ai une note de £5. Je dépense 3,20£. Combien d’argent dois-je laissé?
en montrant aux enfants ce problème, un enseignant demanderait probablement quelle opération les enfants doivent faire: ajouter, soustraire, multiplier ou diviser?, Ils peuvent alors leur demander d’écrire la phrase numérique qu’ils effectueront pour résoudre le problème, qui serait:
£5 – £3.20 =

Les enfants peuvent également rencontrer des phrases numériques avec des lacunes. Dans L’étape clé 1, Ils peuvent rencontrer quelque chose comme ceci:
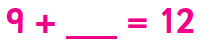
et être invités à déterminer ce qui se passe dans l’écart.,
ceux – ci deviendront progressivement plus difficiles à L’étape clé 2, par exemple:
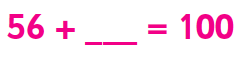
parfois, les enfants recevront des phrases numériques où il y a deux opérations de chaque côté, par exemple:
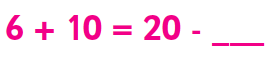
ici, ils doivent comprendre que puisque 16, le côté droit doit être égal à la même quantité, puisque 20-4 = 16, le nombre dans l’écart devrait être 4.,
on peut leur donner une phrase numérique comme celle ci-dessus, mais là où il n’y a pas une réponse à mettre dans l’écart:

ici, il peut être judicieux d’essayer un nombre dans le premier écart, par exemple, 10:




