Comment puis-je savoir quand utiliser le test t à la place du z-test?
Juste au sujet de chaque étudiant en statistiques, je n’ai jamais enseigné m’a demandé cette question à un certain point., Quand j’ai commencé à donner des cours, j’expliquais que cela dépend du problème et que je commençais à discuter du théorème central limite jusqu’à ce que leurs yeux se glacent. Puis j’ai réalisé, c’est plus facile à comprendre si je fais juste un organigramme. Donc, c’est ici!
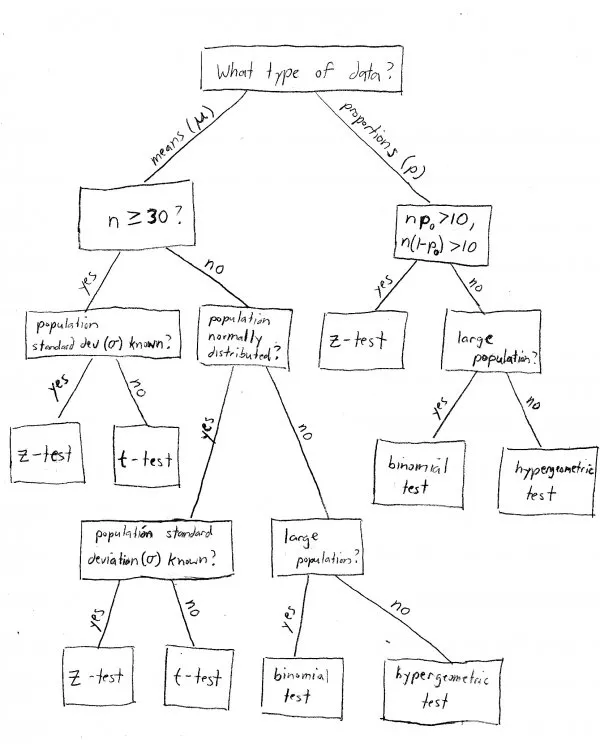
en gros, cela dépend de quatre choses:
- Si nous travaillons avec une moyenne (par exemple, « 37 étudiants ») ou un pourcentage (par exemple, « 15% de tous les élèves »).
- si nous connaissons ou non l’écart type de la population (\(\sigma\))., Dans la vraie vie, nous ne le faisons généralement pas, mais les cours de statistiques aiment résoudre les problèmes là où nous le faisons.
- Si la population est normalement répartie ou non. Ceci est principalement important lorsqu’il s’agit de petits échantillons.
- La taille de notre échantillon. Le nombre magique est généralement 30-ci-dessous qui est considéré comme un « petit » échantillon, et 30 ou plus est considéré comme « grand ». Lorsque la taille de l’échantillon est grande, le théorème central limite nous dit que nous n’avons pas à nous soucier de savoir si la population est normalement distribuée ou non.,
de manière générale, le problème vous dira explicitement si l’écart type de la population est connu – s’ils ne le disent pas, supposons qu’il est inconnu. Il en va de même pour une population normalement distribuée – s’ils ne disent pas « supposons que la population est normalement distribuée », ou quelque chose à cet effet, alors ne faites pas simplement cette hypothèse. Heureusement, si la taille de l’échantillon est assez grande, peu importe!
commencez avec un professeur de statistiques à IU aujourd’hui!




