Dessiner un cercle avec un diamètre (tout le chemin à travers le cercle) de 1
Ensuite, la circonférence (tout le chemin autour du cercle) est 3.14159265… un nombre connu sous le nom Pi
Pi (prononcé comme « tarte ») est souvent écrite en utilisant le symbole grec π
La définition de π est:
La Circonférence
divisé par le Diamètre
d’un Cercle.,
La circonférence divisée par le diamètre d’un cercle est toujours π, peu importe comment grand ou petit le cercle est!
Pour vous aider à vous rappeler ce que π est … dessinez simplement ce diagramme.
trouver Pi vous-même
dessinez un cercle ou utilisez quelque chose de circulaire comme une plaque.,
Mesurer autour de l’arête (la circonférence):

je suis à 82 cm
Mesurer à travers le cercle (diamètre):

j’ai 26 cm
Diviser:
82 cm / 26 cm = 3.1538…
C’est assez proche de π. Peut-être si je mesurais plus précisément?,
Utilisation de la Pi
On peut utiliser π pour trouver une Circonférence quand on sait que le Diamètre
Circonférence = π × Diamètre
on peut Aussi utiliser π pour trouver un Diamètre lorsque nous savons que la Circonférence
Diamètre = Circonférence / π
Rayon
Le rayon est la moitié du diamètre, donc on peut aussi dire:
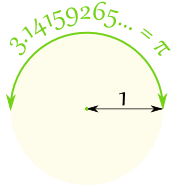
Pour un cercle de rayon 1
La distance à mi-chemin autour du cercle est π = 3.14159265…
Chiffres
π est approximativement égale à:
3.,14159265358979323846<
Les chiffres continuent sans motif.
π a été calculé à cinquante billions de décimales et encore il n’y a pas de modèle pour les chiffres
Approximation
Un moyen rapide et facile approximation de π est 22/7
22/7 = 3.1428571…
Mais comme vous pouvez le voir, 22/7 n’est pas exactement correct. En fait π n’est pas égal au rapport de deux nombres, ce qui en fait un nombre irrationnel.
Une très bonne approximation, meilleure que 1 partie sur 10 millions, est:
355/113 = 3.1415929…,
(think « 113355 », slash the middle « 113/355 », then flip « 355/113 »)
Summary:
| 22/7 | = | 3.1428571… |
| 355/113 | = | 3.1415929… |
| π | = | 3.14159265… |
Remembering The Digits
I usually just remember « 3.,14159 », mais vous pouvez également compter les lettres de:
« puis-je avoir un grand récipient de beurre d’aujourd’hui »
3 1 4 1 5 9 2 6 5
À 100 Décimales
Voici π avec les 100 premières décimales:
3.14159265358979323846264338327950288
4197169399375105820974944592307816
4062862089986280348253421170679…
calculer Pi vous-même
Il existe de nombreuses méthodes spéciales utilisées pour calculer π et en voici une que vous pouvez essayer vous-même: elle s’appelle la série Nilakantha (d’après un mathématicien indien qui a vécu dans les années 1444-1544).,
Il se passe toujours et a ce modèle:
3 + 42×3×4 − 44×5×6 + 46×7×8 − 48×9×10 + …
(Notez le motif + et−, ainsi que le motif des nombres sous les lignes.)
Il donne ces résultats:
| Terme | Résultat (à 12 décimales) |
|---|---|
| 1 | 3 |
| 2 | 3.166666666667 |
| 3 | 3.133333333333 |
| 4 | 3.145238095238 |
| … | … etc! …, |
Obtenir une calculatrice (ou utiliser une feuille de calcul) et de voir si vous pouvez obtenir de meilleurs résultats.







