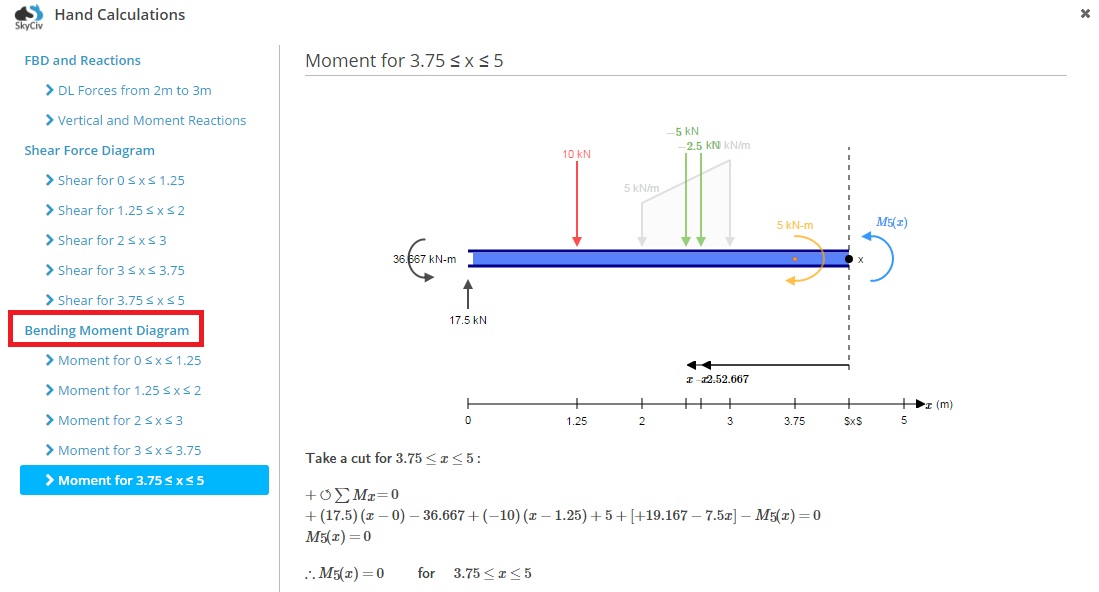
comment calculer le diagramme de moment de flexion d’une poutre
Voici des instructions simples sur la façon de calculer le diagramme de moment de flexion d’une poutre simplement prise en charge. Étudiez cette méthode car elle est très polyvalente (et peut être adaptée à de nombreux types de problèmes différents. La capacité de calculer le moment d’une poutre est une pratique très courante pour les ingénieurs en structure et apparaît souvent dans les examens collégiaux et secondaires.
Tout d’abord, qu’est-ce qu’un moment de flexion?, Un instant, c’est une force de rotation qui se produit lorsqu’une force est appliquée perpendiculairement à un point, à une certaine distance de ce point. Il est calculé comme la force perpendiculaire multipliée par la distance du point. Un moment de flexion est simplement la courbure qui se produit dans une poutre en raison d’un moment. Il est important de se rappeler deux choses lors du calcul des moments de flexion; (1) les unités standard sont Nm et (2) la flexion dans le sens horaire est considérée comme négative., Quoi qu’il en soit, avec les définitions ennuyeuses à l’écart, regardons les étapes pour calculer un diagramme de moment de flexion:
calcul des diagrammes de moment de flexion à la main
calculer les réactions aux supports et dessiner un diagramme de corps libre (FBD).
Si vous ne savez pas comment déterminer les réactions sur les supports, veuillez d’abord consulter ce tutoriel. Une fois que vous avez les réactions, dessinez votre diagramme de corps libre et le diagramme de force de cisaillement sous la poutre., Enfin, le calcul des moments peut se faire en suivant les étapes suivantes:
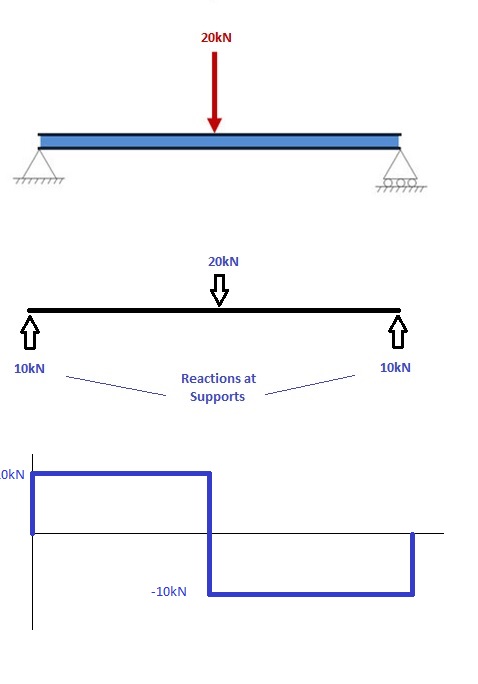
de gauche à droite, faire des « coupes” avant et après chaque réaction/charge
pour calculer le moment de flexion d’une poutre, il faut le diagramme de force de cisaillement. À partir de x = 0, nous allons traverser la poutre et calculer le moment de flexion à chaque point.
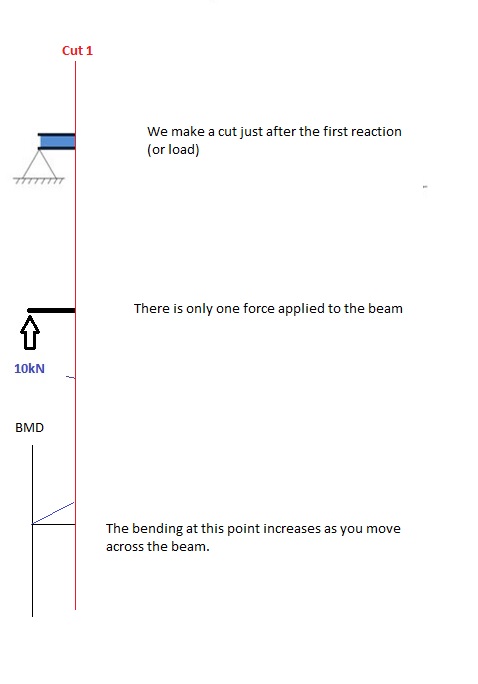
Couper 1
Faire une « coupe” juste après la première réaction de la poutre., Dans notre exemple simple:
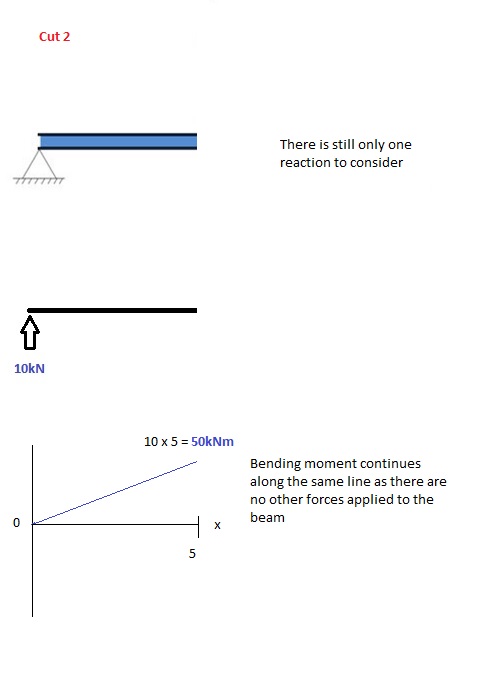
Coupe 2
Cette coupe est faite juste avant la deuxième force le long de la poutre. Comme il n’y a pas d’autres charges appliquées entre la première et la deuxième coupe, l’équation du moment de flexion restera la même., Cela signifie que nous pouvons calculer le moment de flexion maximum (dans ce cas au milieu, ou x = 5) en substituant simplement x=5 dans l’équation ci-dessus:
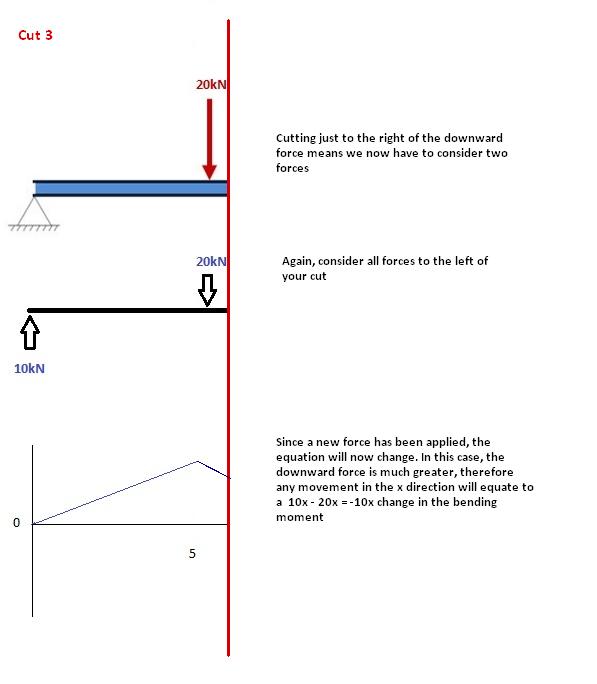
Cut 3
Cette coupe est faite juste après deuxième force le long de la poutre. Maintenant, nous avons deux forces qui agissent à gauche de notre coupe: une réaction de soutien de 10KN et une charge d’action descendante de-20kn. Alors maintenant, nous devons considérer ces deux forces que nous progressons le long de notre faisceau., Pour chaque mètre que nous traversons la poutre, il y aura un moment +10knm ajouté à partir de la première force et-20knm à partir de la seconde. Donc, après le point x=5, Notre équation du moment de flexion devient: M ( x) = 50 +10(x-5) – 20(x-5) M(x)=50 -10(x-5) pour 5 ≤ x ≤ 10 remarque: la raison pour laquelle nous écrivons (x-5) est parce que nous voulons connaître la distance du pt x = 5 seulement. Tout ce qui précède utilise une équation précédente.
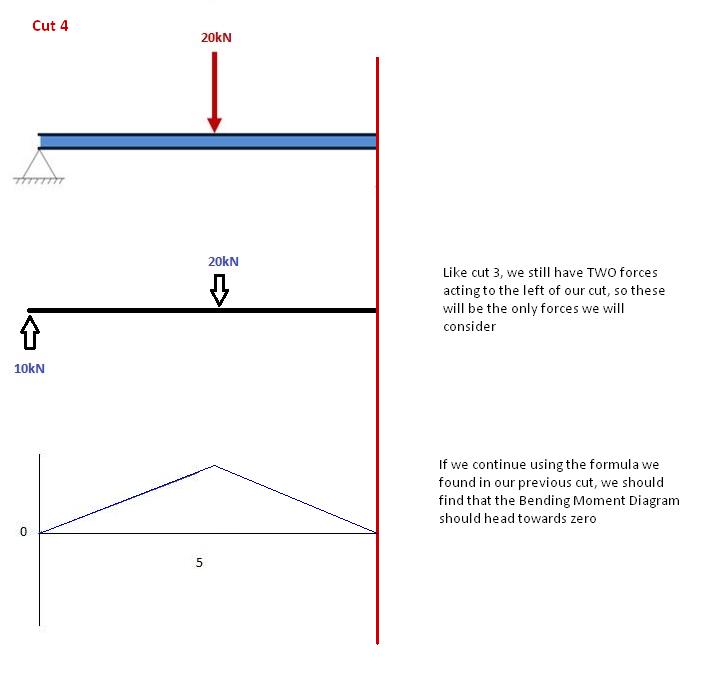
Couper 4
Encore une fois, nous allons passer à travers à la droite de la poutre et de faire une coupure juste avant notre prochaine de la force., Dans ce cas, notre prochaine coupe aura lieu juste avant la réaction du Support droit. Comme il n’y a pas d’autres forces entre le support et notre coupe précédente, l’équation restera la même: M(x) = 50 -10(x-5) pour 5 ≤ x≤ 10 et remplaçons x=10 pour trouver le moment de flexion à la fin de la poutre: M(x) = 50 – 10(10-5) = 0kNm cela est parfaitement logique. Puisque notre faisceau est statique (et non en rotation), il est logique que notre faisceau ait un moment nul à ce stade lorsque nous considérons toutes nos forces., Il satisfait également une de nos conditions initiales, que la somme des moments à un support est égale à zéro. Remarque: Si vos calculs vous conduisent à un autre nombre que 0, Vous avez fait une erreur!
BONUS: Comment calculer la flexion à l’aide d’SkyCiv Faisceau
SkyCiv a un moment de flexion de la calculatrice pour le calcul du moment de flexion diagrammes rapidement et facilement., Sous notre version payante, la calculatrice vous montrera même les calculs complets de la main, montrant les étapes prises pour calculer à la main vos diagrammes de moment de flexion. Modélisez simplement votre faisceau à l’aide de la calculatrice et appuyez sur Résoudre. Il va vous montrer étape par étape les calculs de la façon de dessiner un moment de flexion diagramme (y compris les réductions):